Lösungsstrategie 1:

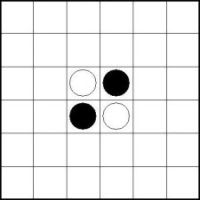
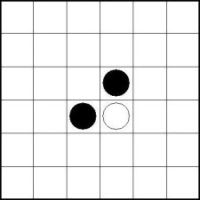
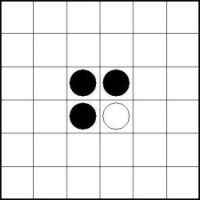
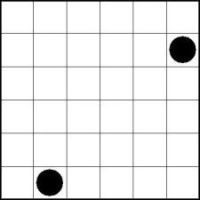
Bei einem 2x2 Feld kann keine der folgenden Besetzungen vorliegen:

Begründung:
Die beiden schwarzen Kreise des vorgegebenen 2x2 Feldes müssen nach den Regeln horizontal bzw. vertikal durch weitere schwarze Kreise verbunden sein. Bei jeder möglichen Verbindung der beiden vorgegebenen schwarzen Kreise können aber die beiden vorgegeben weißen Kreise nicht mehr verbunden werden, da immer einer der beiden weißen Kreise von schwarzen Kreisen umschlossen wird.

Lösungsstrategie 2:

Liegen zwei Kreise gleicher Farbe am Rand des Spielfelds, so müssen diese auch entlang des Randes verbunden sein.

Begründung:
Man nimmt zunächst an, dass die beiden abgebildeten schwarzen Kreise nicht entlang des Randes verbunden werden können. Dann muss in jeder Richtung mindestens ein weißer Kreis zwischen den beiden schwarzen Kreisen auf dem Rand liegen. Bei jeder möglichen Verbindung der beiden vorgegebenen schwarzen Kreise können dann die beiden weißen Kreise aber nicht mehr verbunden werden, da das Spielfeld durch die schwarzen Kreise in zwei Teile zerlegt wird und jeder Teil jeweils nur einen der beiden weißen Kreise enthält. Somit müssen die zwei vorgegebenen schwarzen Kreise entlang des Randes verbunden sein.

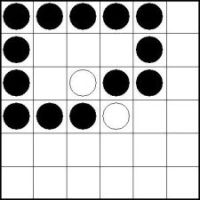
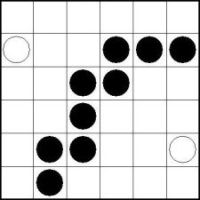
Beispiel:
Hier gibt es genau eine Möglichkeiten die beiden schwarzen Kreise entlang des Randes zu verbinden:

Lösungsstrategie 3:

Die folgenden Aussagen gelten für jedes Spielfeld mit geraden Seitenlängen:
a) Auf dem Rand müssen mindestens zwei schwarze und zwei weiße Kreise liegen.
b) Zählt man von einer Ecke aus die gleichfarbigen Kreise längs einer Seite bis zu einem Farbwechsel, so erhält man immer eine ungerade Zahl.

Begründung:
Zunächst werden alle Gitterkreuze abwechselnd rot und grün eingefärbt. Sind die vier Ecken des Spielfelds rot gefärbt, gibt es insgesamt einen roten Punkt mehr als grüne Punkte. (Begr.: Entfernt man den roten Punkt aus der Mitte, so besteht das Spielfeld aus konzentrischen Quadraten mit gleich vielen roten und grünen Punkten.)

Färbt man die Randlinie aller schwarzen Kreise blau, so ergibt sich ein geschlossener Streckenzug. (Begr.: Alle schwarzen und weißen Kreise bilden jeweils zusammenhängende Gebiete.) Beim Streckenzug wechseln sich immer rote und grüne Punkte ab und aufgrund von Lösungstipp 1 wird kein Punkt doppelt besucht. Deshalb liegen genauso viele rote wie grüne Punkte auf dem Streckenzug.

Wegen Regel 3 enthält der Streckenzug auch alle roten und grünen Punkte, die nicht auf dem Rand des Spielfeldes liegen. Diese Punkte enthalten einen roten Punkt mehr als grüne Punkte. Darum müssen die Punkte, durch die der Streckenzug am Rand geht, einen grünen Punkt mehr als rote Punkte besitzen. Der Streckenzug muss also auf dem Rand bei einem grünen Punkt beginnen und enden. Somit kann ein Wechsel von schwarz nach weiß oder umgekehrt am Rand nur bei einem grünen Punkt stattfinden und der Streckenzug muss durch mindestens drei Randpunkte gehen.

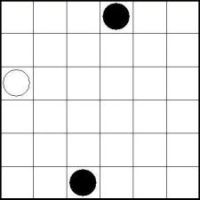
Beispiel:
Hier können noch schwarze und weiße Kreise ergänzt werden:

Autor: Martin Hintermeier